Symbolic Dynamics

[Symbolic Dynamics.pdf](Resources/Symbolic Dynamics.pdf)

https://en.wikipedia.org/wiki/Erlangen_program

Limits

Commonly used ultimately equal parts:

1. Consider a slice of a unit circle, where h is the line across the arc, φ the angle.
2. Given a triangle, draw a perpendicular from a vertex. The area of the original is ultimately equal to the new one given by (as long as both edges are infinitesimal).

Curvature

Internal curvature

Define the angular excess for polygons.

In constant curvature,

Generalizing, (Limit of angular excess per unit area at p).

So

Circle of curvature

Characterizations of curvature in 2D:

.

If tangent is horizontal, Taylor’s theorem implies . In general, .

Even more generally, for non-unital speeds we have for .

Euler’s curvature formula

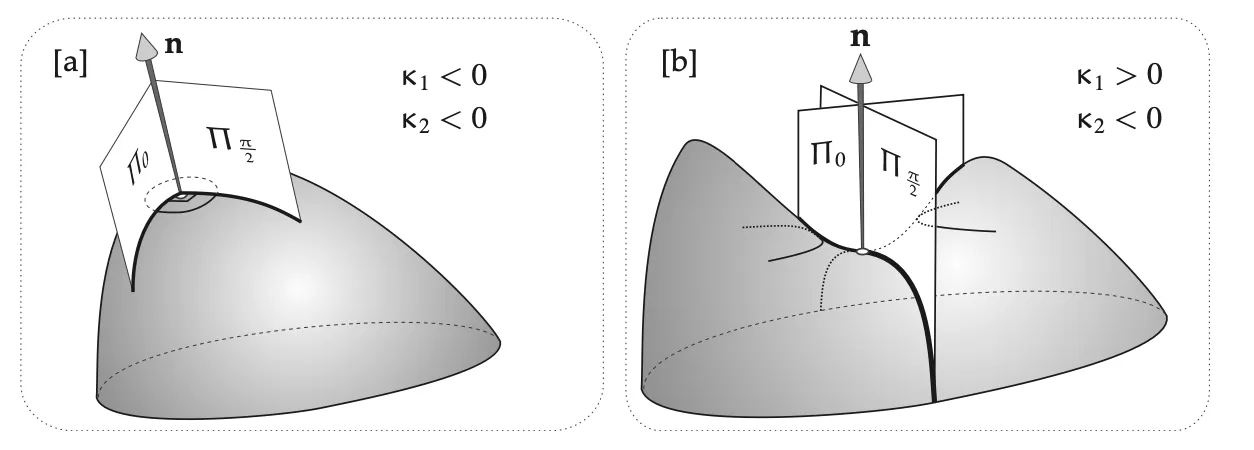
Given a point p and direction, we can erect the normal section spanned by and . At p, we can then describe curvature via . Let be the max and min curvatures, choose to coincide with the direction of . These two principal directions are perpendicular and . When the point is called umbilic and surface locally resembles a sphere. When = 0, see 12.4.

WARNING

Locally the surface can be represented by by appropriate choise of axis. Slicing through the surface with tangent planes parallel to Tp, (it turns out) the curves are conic sections (ellipse if κ1,2 share a sign and hyperbola otherwise). Moreover, the quadratic equation is homogenous: ( produces another solution), so the shape is unaffected by height. Thus the conics all share two perpendicular axes of symmetry. Aligning our coordinate system with these axis, our local equation becomes . And the curvature of our parabola in the plane y=0 is . Finally, for a general angle, which comes out to our result after plugging in.

(Source)

Decomposition of a line curve

We want to consider the component of our osculating plane in the surface. See.

Locally, our curve is a circle in the osculating plane P, containing our curvature vector . Next, the acceleration of the projection = projection of acceleration. It follows that in the diagram . Note that in general the projected curve is not traversed at unit speed so the projected acceleration has a component tangential to (projected curve). However, at p, the point and its projection are the same speed.

Considering the projections onto the geodesic plane (tangent plane of surface) and the normal section.

It follows , providing the decomposition .

( is spanned by the surface normal and the tangent.)

Note that all lie in the same (BN) plane!.

All the curves passing through a point in the same direction have the same where n is the rate of change of the surface normal in the T direction (See).

REMARK

Note that and are different - otherwise . They coincide on a geodesic. Curves with the same normal curvature are differentiated by their geodesic curvatures. By considering the curves created by intersecting an osculating plane in various angles rotated around , one gets a set of curves of increasing geodesic curvature.

Also important to note that does not lie in the normal section in general. This is only true for a principal curvature. i.e. on an ellipse, it’s clear that off an axis, the surface pares away to the side, causing normal to turn outwards. Also evident from a non-closed ellipse geodesic, has to shift along .

So only along a principal curvature the osculating plane approximation is locally “faithful” to the actual curve in reflecting the actual change in normal.

Geodesics

On a geodesic, coincides with tension Fp which is contained in the osculating plane so the geodesic curvature vanishes. Locally the intersection of the normal section with the surface.

On a oblong ellipse (i.e. earth), the meridians and equator are the only closed geodesics.

REMARK

Principal curvatures restrict T while geodesics restrict . There is a geodesic through every direction, and multiple curves governed by the direction of the normal for every principal direction. i.e. .

Traveling a geodesic along a principal direction, and hence stays in the same initial normal section globally. For a general principal curve, the geodesic curvature causes the tangent to deviate from the section. (Do third order effects matter?)

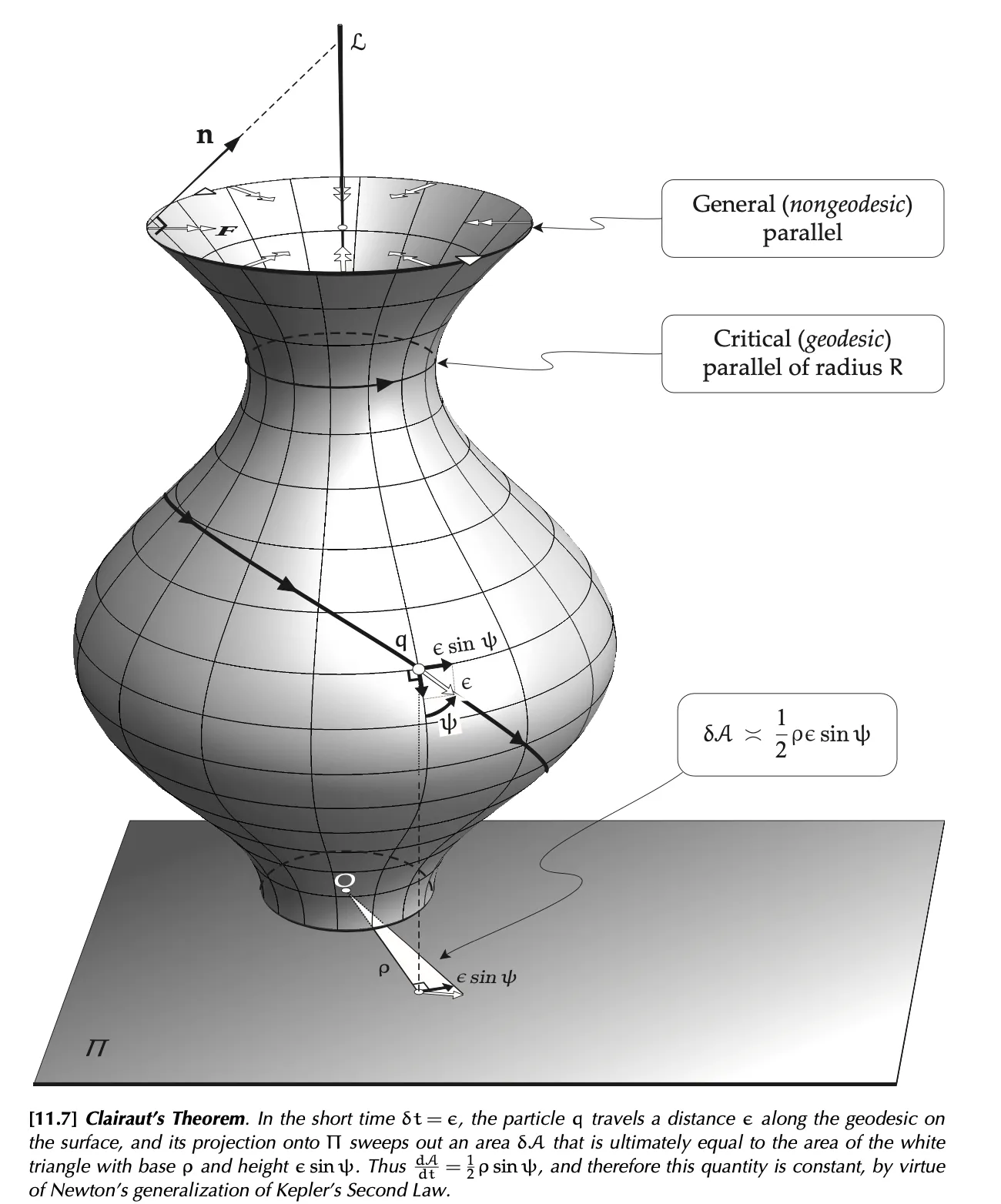
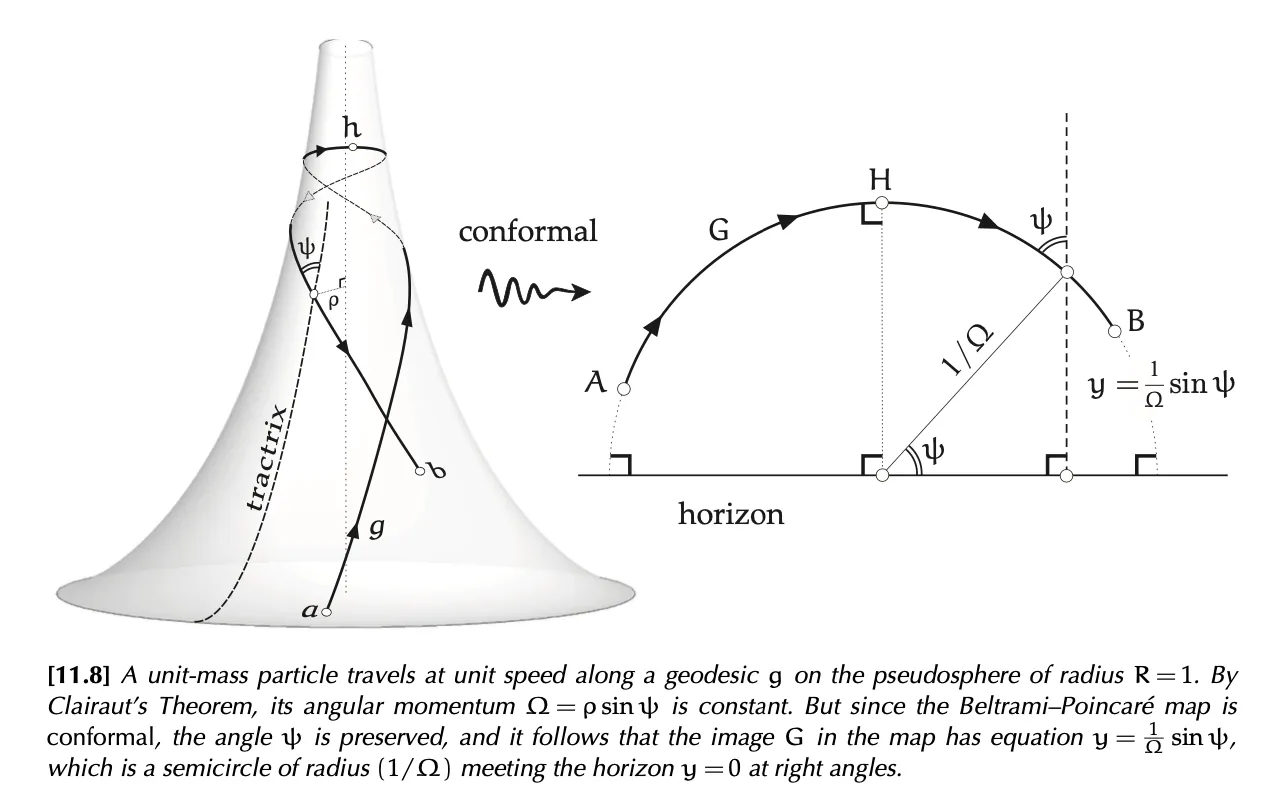
Clairut

Extrinsic curvature

Normal map.

Polyhedral: Consider a point on each side of a polygon adjacent to a vertex, arranged such that the perpendicular lines from each point to the 2 neighboring sides connect up between points. Then . And

Shape operator

For a unit vector v in , is defined as the directional derivative of along the arc formed by dropping a perpendicular from p+v to . For non-unit vectors, . This makes sense if we think of as velocity, so that gives the change wrt time.

REMARK

Given a differentiable function of t, interpreted as a function of surface distance s via unit speed velocity, it can also be interpreted as a function from the tangent space since . Both derivatives can be calculated via pullbacks .

The shape operator approximates how the normal vector changes as we move . It is defined . This is a linear operator on .

Along a principal direction (since ) this is just (See). So the principal directions are the eigenvectors.

SF2

Moreover, .

PROOF

Project onto normal section Alternatively, . Alternatively apply Euler’s formula.

In an arbitrary orthogonal basis, . Another way to view it is that SF2 determines the entries of S. Geometrically, the two components of measure the curvature of within , and projected onto resp. (See)